di Ing. Saverio Arcuraci
Come noto, l’iter procedurale per la realizzazione del ponte sullo Stretto di Messina va avanti, e parallelamente sui social si innescano spesso discussioni che investono l’ambito tecnico relativamente all’opera, in particolare in molti si pongono la domanda:
“Ma il ponte, come si comporterà quando sarà soggetto ai venti presenti sullo Stretto?”
Analizzare a fondo il problema richiede conoscenze nell’ambito dell’analisi strutturale e di fluidodinamica, cercherò di spiegare in modo semplice, senza appesantire troppo l’articolo.
Possiamo dire che in generale, ogni struttura (sia essa un edificio o un ponte) possiede un certo numero di gradi di libertà di movimento; ad esempio se consideriamo un edificio di quattro piani, per ogni piano abbiamo, facendo le dovute approssimazioni e ipotizzando che i solai rimangano sempre paralleli tra loro (si ipotizzano quindi travi con elevatissima rigidezza torsionale), due gradi di libertà traslazionali (lungo assi X e Y di un piano di riferimento cartesiano) ed un grado di libertà rotazionale, quindi tre gradi di libertà, da considerare ad esempio, in caso di sisma. Ogni piano può essere considerato quindi, come fosse composto da tre oscillatori, e nel caso di quattro piani abbiamo 3 x 4 = 12 gradi di libertà complessivi.
Partendo da questo presupposto, si possono ricavare le frequenze proprie di ogni struttura (per ogni grado di libertà otteniamo una frequenza propria, ovvero un modo di vibrare) scrivendo l’equazione del moto di ogni oscillatore e mettendo a sistema:

Quella che precede è la consueta forma di rappresentazione, in termini matriciali, di un sistema di equazioni del moto, una per ogni oscillatore, sono equazioni differenziali del secondo ordine, e considerando le semplici oscillazioni libere (sistema non forzato e non smorzato), utilizzando l’analisi modale (per sapere come si fa, rimando i lettori ad un libro di analisi sismica delle strutture) è possibile ricavare le frequenze proprie di oscillazione della struttura. Queste hanno valori che, possiamo dire, rappresentano l’impronta digitale della struttura stessa, non sono modificabili, a meno che non si apportino, ad esempio, delle variazioni sulla rigidezza degli elementi strutturali, travi e pilastri.
È utile ricordare che i progettisti si riferiscono principalmente ai primi modi di vibrare, cioè ai periodi più alti.
Analogamente, anche nei ponti sospesi è possibile, partendo dai gradi di libertà del sistema, ricavare le frequenze proprie di oscillazione, ma a che ci servono? Perché ci affanniamo a svolgere questi calcoli?
Facciamo un esempio banale, ipotizziamo un sistema ad un solo grado di libertà di movimento, come un’altalena (Fig. 1):

Un’altalena è un sistema assimilabile ad un pendolo e del quale possiamo ricavare il periodo proprio (l’unico perché abbiamo un solo grado di libertà), e quindi la frequenza propria di oscillazione:
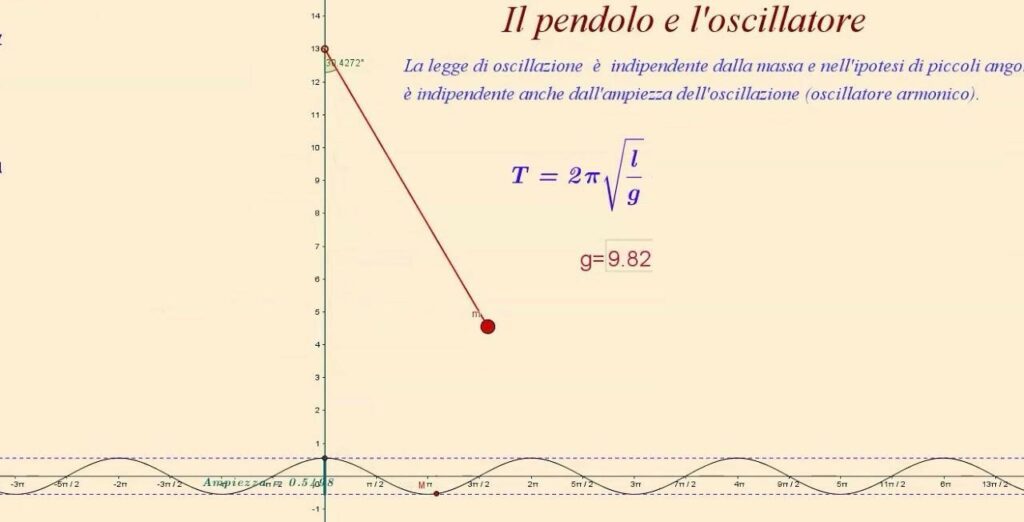
La frequenza propria si calcola con:
f=1/T
dove T è il periodo, l rappresenta la lunghezza del filo e g l’accelerazione di gravità.
Cosa fa il bimbo per incrementare l’ampiezza dell’oscillazione? Fornisce una spinta ritmica con le gambe (da bambini l’abbiamo fatto tutti) con una frequenza che è identica a quella propria dell’oscillatore (e logicamente in fase).
In sintesi, il bimbo sta mandando in risonanza il sistema. Mettete bene a mente la parola “risonanza”, questo è un termine che fa venire l’orticaria agli ingegneri, soprattutto strutturisti, meccanici, aerospaziali.
Gli ingegneri devono progettare la loro opera in modo tale che questa non si trovi mai a subire fenomeni di risonanza durante il normale esercizio o in caso di eventi naturali; per un edificio vuol dire che dovrò progettarlo in modo che abbia le frequenze proprie diverse da quelle, ad esempio, generate da eventi sismici, potrò utilizzare anche artifizi come isolatori sismici che modificano profondamente le frequenze proprie della struttura stessa.
E per i ponti? Anche queste strutture hanno più gradi di libertà, l’impalcato subisce spostamento orizzontale, nonché fenomeni flessionali e torsionali.
Come detto, anche per i ponti possiamo ricavare, utilizzando le relative equazioni, le frequenze proprie di oscillazione, in questo articolo ci concentreremo su due valori in particolare, il primo periodo di oscillazione flessionale e il primo periodo di oscillazione torsionale, tra poco vedremo perché.
Ma innanzitutto, cos’è che principalmente sollecita un ponte sospeso? La forzante per eccellenza è il vento.
Il vento genera dei moti turbolenti sull’impalcato, e riveste notevole importanza il fenomeno del distacco dei vortici:
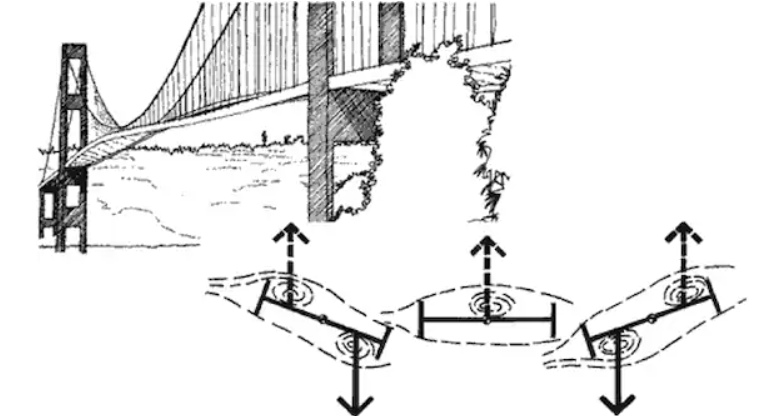
Questo fenomeno si genera quando un fluido investe un corpo, e quindi si innesca una scia di vortici (governata dalla forma del corpo stesso e dal numero di Reynolds) che si distaccano con una certa frequenza. Riferendoci ad un ponte sospeso, se questa frequenza è molto vicina alle frequenze proprie dell’impalcato, si può innescare il fenomeno della risonanza (sempre lei!!).
Il Flutter
Con flutter si intende un fenomeno di instabilità aeroelastica dovuta ad autoeccitazione della struttura. A causa del vento ed a causa di distacco asimmetrico dei vortici, la struttura (nel nostro caso continuiamo a riferirci all’impalcato di un ponte sospeso) inizia ad oscillare, sia verticalmente che torsionalmente. Tale fenomeno dipende anche dalle variazioni delle forze aerodinamiche che patisce l’impalcato a causa delle sue stesse oscillazioni che si sono innescate. Nel caso in cui il rapporto tra i valori del primo periodo flessionale e del primo periodo torsionale, sia vicino ad 1, si hanno maggiori probabilità di avere instabilità per flutter. Ma attenzione, ogni impalcato ha proprie caratteristiche strutturali, dalle quali dipende la risposta della struttura, e soprattutto dipende la velocità critica dei venti per instabilità da flutter.
Il ponte sullo Stretto di Messina
Quanto detto fin adesso, in linee generali, ma torniamo al nostro ponte sullo Stretto di Messina. Sappiamo che il primo periodo flessionale ha valore di circa 17 secondi (modo longitudinale antisimmetrico) mentre il primo periodo torsionale ha valore di 12 secondi (modo torsionale antisimmetrico), otteniamo un rapporto di 1.41 (qualcuno ha ottenuto 1.36, ma cambia poco).
Abbiamo già parlato delle caratteristiche smorzanti dell’impalcato tricassone a profilo aerodinamico soprannominato Messina Type Deck; sappiamo che questo tipo di struttura (impalcato di terza generazione) presenta una modestissima resistenza al vento, ma è anche estremamente affidabile nei confronti dell’instabilità aeroelastica (flutter). In particolare, ingegneri che stanno lavorando al progetto, hanno ricavato una stima di velocità dei venti per instabilità da flutter in un range compreso tra 85 e 91 m/sec, venti tipici di uragani forza 4 o 5, che lo Stretto non vedrà mai.
Ma senza andare troppo lontano, già il Cowi ci aveva rassicurato:
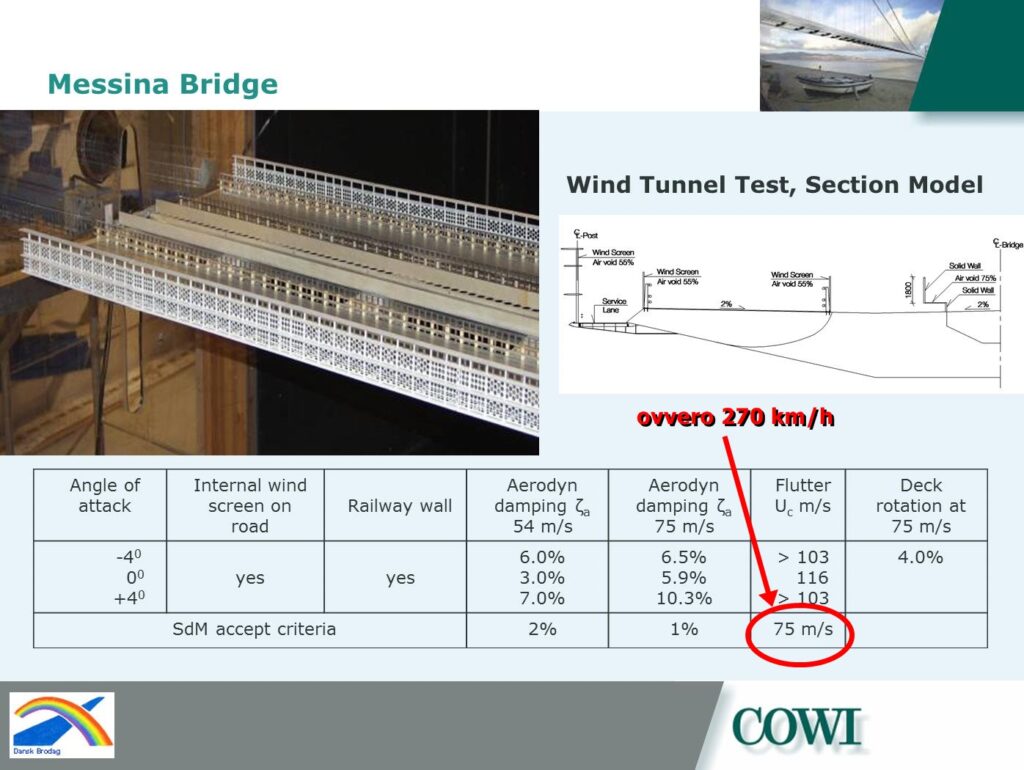
Certamente, se i progettisti o il Comitato Tecnico Scientifico avessero avuto dei dubbi sull’affidabilità dell’opera e sulla risposta ai venti, non saremmo qui a discutere di ponte sullo Stretto.
Attendiamo il progetto esecutivo, ci vediamo sul ponte.







